|
|
Quelques
exemples d'utilisation
1 - Suivi et localisation
d'une cible complexe, connue a priori, par vision monoculaire
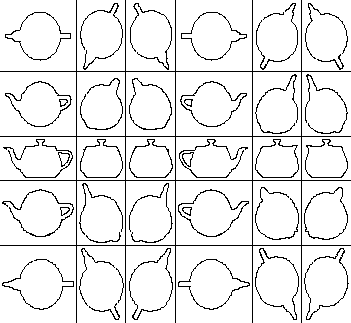
1 - Suivi et localisation d'une cible complexe, connue a priori, par vision monoculaire Le suivi et la localisation d'une cible se fait à l'aide d'une caméra 2D. L'objet est connu a priori, mais aucune hypothèse n'est faite sur son mouvement (mouvement saccadé possible). Les six degrés de liberté d'un corps rigide en mouvement accéléré doivent être considérés. La méthode proposée se base sur une modélisation de la cible par graphe d'aspect. Une représentation originale des modèles 2D du graphe d'aspect a été développée. Associée à une analyse en composantes principales, elle permet de retrouver la pose de la cible de manière très efficace. L'algorithme proposé est aussi bien utilisé pour l'initialisation que pour la poursuite. Il permet aussi de bien tenir compte des contraintes très générales qui sont imposées. Aujourd'hui, la capacité de traitement d'information des ordinateurs permet d'analyser des problèmes complexes en temps réel. La vision par ordinateur a particulièrement profité de ces progrès. En effet, des tâches telles que le téléguidage de robot, la télé-surveillance des autoroutes (pour la vérification automatique du trafic) ou encore la supervision de chaînes de production sont rendues possibles. De nombreux problèmes restent cependant encore du domaine de la recherche. L'un d'eux est le suivi et la localisation d'objet. Il s'agit d'un point très important puisqu'il est indispensable pour toutes sortes d'applications. Le guidage automatique de véhicule, par exemple, nécessite la connaissance exacte de la position des obstacles. L'estimation de la position exacte d'un objet est un problème générique complexe. Les approches sont très différentes suivant la connaissance a priori de l'objet ou non, le type de capteurs utilisés (une ou plusieurs caméras 2D, caméras 3D, etc.), et le type de déplacement. Dans la recherche que nous proposons, il s'agit de retrouver la position 3D d'un objet connu, rigide et « relativement complexe », à l'aide d'une caméra 2D fixe. Le mouvement de l'objet peut être saccadé et des occlusions partielles peuvent se produire. L'application pratique liée à cette étude est le remplacement d'isolateurs sur les lignes électriques. L'opérateur, dans un camion au niveau du sol, commande deux bras manipulateurs rattachés au véhicule par une nacelle, sur laquelle se trouvent des capteurs. Ces capteurs envoient à l'opérateur une image qui lui permet de remplacer les isolateurs. L'image n'est cependant pas stabilisée par rapport au mouvement de la nacelle. L'opérateur peut donc éprouver des difficultés à guider les bras. À l'aide d'une caméra 2D observant la scène, l'algorithme proposé devra permettre de connaître la position de la nacelle et ainsi de compenser le mouvement de celle-ci pour que l'image reçue par l'opérateur soit stable. Le problème qui se pose se résume donc à trouver la position dans l'espace d'un objet, à partir d'une séquence d'images 2D. Les algorithmes classiques [1,5,6,7], utilisés pour la poursuite de cible, nécessitent toujours une étape de prédiction afin de limiter les recherches dans l'espace des poses possibles. Cette étape de prédiction peut être plus ou moins complexe et va de l'utilisation de la pose de l'objet dans l'image précédente [6] à de pseudo-filtres de Kalman très élaborés [5]. L'estimation initiale de la pose obtenue par cette étape de prédiction sert ensuite de point de départ à des algorithmes de raffinement de pose. Malheureusement, dans notre cas, avec le manque de contraintes imposées au mouvement de la cible, aucune prédiction ne pourrait donner une bonne estimation initiale de la pose. Or les algorithmes itératifs permettant de raffiner la pose convergent d'autant plus rapidement et d'autant mieux que l'estimation initiale est bonne (cf. [2]). Afin de résoudre ce problème, une approche originale basée sur une modélisation par graphe d'aspect de la cible est proposée. Chaque modèle 2D du graphe d'aspect est représenté d'une part par une image binaire qui contient le contour de la cible (voir figure 1) et d'autre part par une paramétrisation de type « coordonnées polaires ». La paramétrisation permet d'effectuer une analyse en composantes principales et ainsi de diminuer énormément la taille de l'espace de paramétrisation. La topologie naturelle (basée sur la distance euclidienne) de l'espace des paramétrisations représente une bonne méthode de comparaison entre les différentes formes des modèles du graphe d'aspect. Une classification en groupe de modèles de même forme peut donc être effectuée sur le graphe d'aspect. Pratiquement la création de tels groupes se fait à l'aide d'un algorithme de type fuzzy K-Means dans l'espace des composantes principales (voir figure 2). Cette classification peut ensuite être utilisée pour simplifier la recherche de la pose de la cible. À cause de la nature « polaire » de la paramétrisation, une rotation dans le plan de l'un des modèles correspond à une permutation circulaire des composantes du vecteur de paramétrisation. Ainsi, en effectuant une transformation de Fourier discrète des vecteurs de paramétrisation avant l'analyse en composantes principales on ajoute une invariance structurelle par rapport aux rotations dans l'espace des composantes principales. La détermination des paramètres de pose de la cible peut être faite de la manière suivante. Deux des paramètres de translation sont retrouvés à partir de la position du modèle 2D dans l'image. Deux des paramètres de rotations sont obtenus à partir du modèle du graphe d'aspect qui a été retenu. Les deux derniers paramètres (le facteur d'échelle et la rotation dans le plan image) peuvent être obtenus directement à l'aide de la paramétrisation des modèles 2D. En effet, dans l'espace des composantes principales un facteur d'échelle correspond tout simplement à une multiplication par un nombre scalaire. L'angle de rotation peut, quant à lui, être obtenu par la phase de la transformée de Fourier. À partir de toutes ces remarques, un algorithme a été élaboré permettant de trouver les poses les plus probables dans l'image 2D. Celles-ci sont ensuite vérifiées en utilisant une approche de l'algorithme de H.T. Huttenlocher [3]. L'hypothèse obtenant la meilleure évaluation est celle qui est retenue. L'avantage de l'approche que nous proposons réside dans les
faibles contraintes imposées au mouvement ou au changement d'aspect
de l'objet. De plus, l'algorithme peut être utilisé aussi
bien lors de l'initialisation, c'est-à-dire lors du calcul de
la pose de la cible dans la première image, que lors de la poursuite
proprement dite. La seule différence réside dans le temps
de calcul puisque au lieu d'effectuer une recherche complète
lors de la poursuite, on se limite à une recherche partielle
autour de la pose trouvée pour l'image précédente.
Figure 1. Graphe d'aspect d'une théière avec 30 modèles.
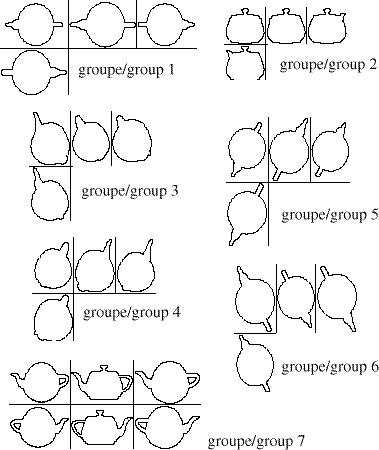
Figure 2. Classification selon la forme pour la théière Référence: Laboratoire de vision et systèmes numériques
2 - Les images multispectrales à plus de trois canaux
Dans l'exemple suivant, l’ACP a porté sur les canaux vert, rouge et proche-infrarouge d'une image SPOT, afin de générer les trois canaux ACP1, ACP2 et ACP3. L’intérêt de l’ACP, pour des images à 3 canaux (comme les données SPOT 1, 2 et 3) est de synthétiser au maximum les images. Ainsi, le premier canal (ACP1), le plus intéressant, présente la brillance globale de l’image, améliorant considérablement les contrastes. Ce canal d’une grande richesse thématique est une bonne représentation synthétique de l’image. Le deuxième (ACP2), rend compte des principales différences spectrales entre les canaux sources. Il est en général très bien adapté à l’étude de la végétation et est assez fortement corrélé avec le canal proche infrarouge et dans une moindre mesure avec l’indice de végétation normalisé. Le troisième (ACP3) est généralement constitué du bruit résiduel, et ne présente que rarement de l’intérêt. Les pixels aberrants ou les défauts des capteurs, qui apparaissent sur ce canal, sont ainsi absents des deux autres.
|
|||||||||||||